Algorithms - Primality Test

Project #1: Primality Test

1. Screenshot of my application

Working example

2. All of the code I wrote

2a. Implementation of modular exponentiation.

def mod_exp(x, y, N):
    if y == 0: return 1
    z = mod_exp(x, int(y/2), N)
    if y % 2 == 0:  # if y is even
        return z**2 % N
    else:
        return (x * z**2) % N

2b. Implementation of the Fermat primality tester.

def fermat(N,k):
    for x in range(k):
        a = random.randint(2, N-1)  # positive integers less than N. a=1 is not useful so not included.
        if mod_exp(a, N-1, N) != 1:
            return 'composite'
    return 'prime'

2c. Implementation of the Miller-Rabin algorithm.

def miller_rabin(N,k):
  for x in range(k):
    a = random.randint(2, N-1)
    if mod_exp(a, N-1, N) == 1:  # starts with Fermat's theorem
      exp = N-1
      while exp % 2 == 0:  # while exponent is even, take divide exponent by 2 (take the square root)
        exp = int(exp/2)
        mod_exp_result = mod_exp(a, exp, N)
        if mod_exp_result != 1:  # first time when mod_exp result is not 1
          if mod_exp_result == N - 1:  # if result is N-1 (mod N) == -1 (mod N)
            return 'prime'
          else:  # if the first non-1 result is not -1, N is composite
            return 'composite'
    else:
      return 'composite'  # if a^(N-1) mod N returns anything else than 1, it is composite.
  return 'prime'  # if all test is passed for k times, N is most likely a prime number.

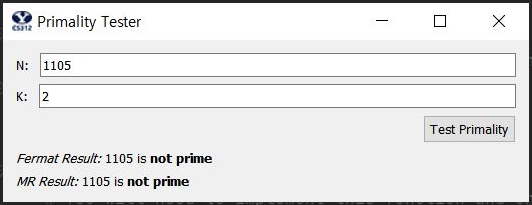
2d. A brief discussion of some experimentation you did to indentify inputs for which the two algorithms disagree and why they do so. Include a screenshot showing a case of disagreement.

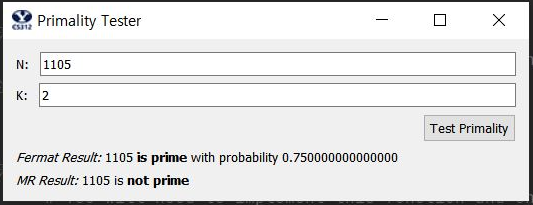
• when I experimented with small numbers for k like 1 or 2 or 3, I could find some cases that fermat says it is prime but miller_rabin says it is composite number.
• for example, 561 or 1105 (another Carmichael number) had that problem.
• non-Carmichael number rarely had errors, but they were more unlikely to have errors than Carmicahel numbers.

Two algorithms showing disagreement

Showing right case even with small number of k

3. Time/ Space complexity

def mod_exp(x, y, N):
    if y == 0: return 1
    z = mod_exp(x, int(y/2), N)
    if y % 2 == 0:  # if y is even
        return z**2 % N
    else:
        return (x * z**2) % N

• Both multiplications of z**2 (z * z) takes O(n^2) time complexity when n is number of bits representing N, and the recursion happens until y == 0, which means log base 2 of y times. Therefore, the whole method takes O(n^2 * log_2 y) time complexity.
  • Since we are mostly setting y to N-1, we could say log_2 y is n, which makes O(n^3) time complexity.
• Each function call will take O(n) space complexity and that stacks up log(n) times which adds up to O(nlogn) space complexity.

def fermat(N,k):
    for x in range(k):
        a = random.randint(2, N-1)  # positive integers less than N. a=1 is not useful so not included.
        if mod_exp(a, N-1, N) != 1:
            return 'composite'
    return 'prime'

• First, the whole thing is repeating k times. And each iteration will have O(n^3) from mod_exp function.
  • Therefore, time complexity of this function is O(n^3)
• Modular exponential’s space complexity was O(nlogn) and it is just repeating it k times, so space complexity stays the same. O(nlogn) space complexity.

def miller_rabin(N,k):
  for x in range(k):
    a = random.randint(2, N-1)
    if mod_exp(a, N-1, N) == 1:  # starts with Fermat's theorem
      exp = N-1
      while exp % 2 == 0:  # while exponent is even, take divide exponent by 2 (take the square root)
        exp = int(exp/2)
        mod_exp_result = mod_exp(a, exp, N)
        if mod_exp_result != 1:  # first time when mod_exp result is not 1
          if mod_exp_result == N - 1:  # if result is N-1 (mod N) == -1 (mod N)
            return 'prime'
          else:  # if the first non-1 result is not -1, N is composite
            return 'composite'
    else:
      return 'composite'  # if a^(N-1) mod N returns anything else than 1, it is composite.
  return 'prime'  # if all test is passed for k times, N is most likely a prime number.

• This function has for loop repeating k times.
• Inside that there is a while loop that repeats log_2 N times. (n)
• inside that while loop, there is mod_exp function that has O(n^3)
  • So, the time complexity of this function is O(n^4)
• Space complexity will be O(n log(n)) as there is nothing much space taken other than repeating the mod_exp function.

4. Probabilities of correctness

• Fermat p
  • I used the probability of getting the error and subtracted it from 1
  • 1 - 1/2**k
• Miller-Rabin p
  • For at least 3/4 of the possible choice of a that will not be the case (which means there might me an error for 1/4 of possible a ’s.
  • 1 - 1/4**k

def fprobability(k):
    return float(1 - 1/2**k) 

def mprobability(k):
    return float(1 - 1/4**k)